머신러닝 - SVC,GridSearchCV
BREAST CANCER CLASSIFICATION
STEP #1: PROBLEM STATEMENT
- 유방암진단 문제 : 양성이냐 악성이냐 예측
-
30 features are used, examples: - radius (반지름) - texture (조직) - perimeter (둘레) - area - smoothness (local variation in radius lengths) - compactness (perimeter^2 / area - 1.0) - concavity (오목함) - concave points (오목한 부분의 점) - symmetry (대칭) - fractal dimension (“coastline approximation” - 1)
- 30 input features
- Number of Instances: 569
- Class Distribution: 212 Malignant(악성), 357 Benign(양성)
- Target class: - Malignant(악성) - Benign(양성)
https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)
STEP #2: IMPORTING DATA
# import libraries
import pandas as pd # Import Pandas for data manipulation using dataframes
import numpy as np # Import Numpy for data statistical analysis
import matplotlib.pyplot as plt # Import matplotlib for data visualisation
import seaborn as sb # Statistical data visualization
# %matplotlib inline
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
cancer.keys()
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])
print(cancer['DESCR'])
.. _breast_cancer_dataset:
Breast cancer wisconsin (diagnostic) dataset
--------------------------------------------
**Data Set Characteristics:**
:Number of Instances: 569
:Number of Attributes: 30 numeric, predictive attributes and the class
:Attribute Information:
- radius (mean of distances from center to points on the perimeter)
- texture (standard deviation of gray-scale values)
- perimeter
- area
- smoothness (local variation in radius lengths)
- compactness (perimeter^2 / area - 1.0)
- concavity (severity of concave portions of the contour)
- concave points (number of concave portions of the contour)
- symmetry
- fractal dimension ("coastline approximation" - 1)
The mean, standard error, and "worst" or largest (mean of the three
worst/largest values) of these features were computed for each image,
resulting in 30 features. For instance, field 0 is Mean Radius, field
10 is Radius SE, field 20 is Worst Radius.
- class:
- WDBC-Malignant
- WDBC-Benign
:Summary Statistics:
===================================== ====== ======
Min Max
===================================== ====== ======
radius (mean): 6.981 28.11
texture (mean): 9.71 39.28
perimeter (mean): 43.79 188.5
area (mean): 143.5 2501.0
smoothness (mean): 0.053 0.163
compactness (mean): 0.019 0.345
concavity (mean): 0.0 0.427
concave points (mean): 0.0 0.201
symmetry (mean): 0.106 0.304
fractal dimension (mean): 0.05 0.097
radius (standard error): 0.112 2.873
texture (standard error): 0.36 4.885
perimeter (standard error): 0.757 21.98
area (standard error): 6.802 542.2
smoothness (standard error): 0.002 0.031
compactness (standard error): 0.002 0.135
concavity (standard error): 0.0 0.396
concave points (standard error): 0.0 0.053
symmetry (standard error): 0.008 0.079
fractal dimension (standard error): 0.001 0.03
radius (worst): 7.93 36.04
texture (worst): 12.02 49.54
perimeter (worst): 50.41 251.2
area (worst): 185.2 4254.0
smoothness (worst): 0.071 0.223
compactness (worst): 0.027 1.058
concavity (worst): 0.0 1.252
concave points (worst): 0.0 0.291
symmetry (worst): 0.156 0.664
fractal dimension (worst): 0.055 0.208
===================================== ====== ======
:Missing Attribute Values: None
:Class Distribution: 212 - Malignant, 357 - Benign
:Creator: Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian
:Donor: Nick Street
:Date: November, 1995
This is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.
https://goo.gl/U2Uwz2
Features are computed from a digitized image of a fine needle
aspirate (FNA) of a breast mass. They describe
characteristics of the cell nuclei present in the image.
Separating plane described above was obtained using
Multisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree
Construction Via Linear Programming." Proceedings of the 4th
Midwest Artificial Intelligence and Cognitive Science Society,
pp. 97-101, 1992], a classification method which uses linear
programming to construct a decision tree. Relevant features
were selected using an exhaustive search in the space of 1-4
features and 1-3 separating planes.
The actual linear program used to obtain the separating plane
in the 3-dimensional space is that described in:
[K. P. Bennett and O. L. Mangasarian: "Robust Linear
Programming Discrimination of Two Linearly Inseparable Sets",
Optimization Methods and Software 1, 1992, 23-34].
This database is also available through the UW CS ftp server:
ftp ftp.cs.wisc.edu
cd math-prog/cpo-dataset/machine-learn/WDBC/
.. topic:: References
- W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction
for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on
Electronic Imaging: Science and Technology, volume 1905, pages 861-870,
San Jose, CA, 1993.
- O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and
prognosis via linear programming. Operations Research, 43(4), pages 570-577,
July-August 1995.
- W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques
to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994)
163-171.
col_names = np.append(cancer['feature_names'],'target')
df = pd.DataFrame(data=np.c_[cancer['data'],cancer['target']],columns=col_names)
# np.c_ 와 np.append
df.columns
Index(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension',
'radius error', 'texture error', 'perimeter error', 'area error',
'smoothness error', 'compactness error', 'concavity error',
'concave points error', 'symmetry error', 'fractal dimension error',
'worst radius', 'worst texture', 'worst perimeter', 'worst area',
'worst smoothness', 'worst compactness', 'worst concavity',
'worst concave points', 'worst symmetry', 'worst fractal dimension',
'target'],
dtype='object')
STEP #3: VISUALIZING THE DATA
# 페어 플롯을 이용해서, 각 컬럼의 관계를 파악하세요.
# 물론 상관계수도 찍어야 합니다.
sb.pairplot(data = df , x_vars=df.iloc[:,:5],y_vars=df.iloc[:,:5],hue='target')
plt.show()
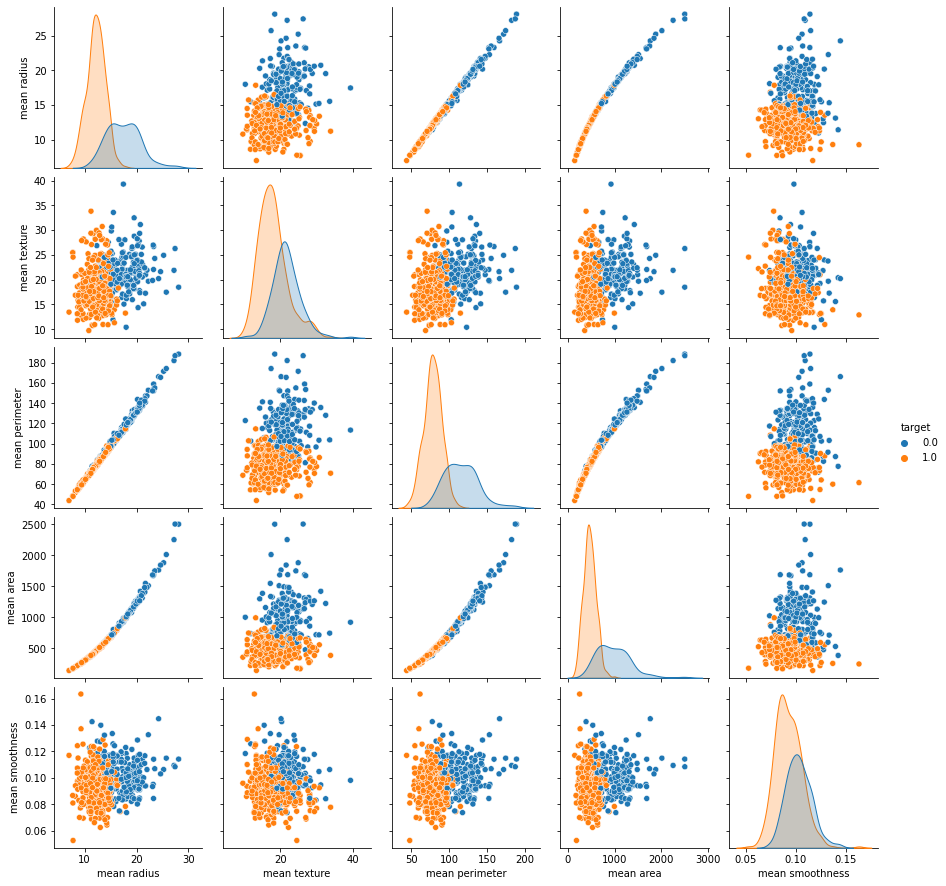
df.iloc[:,:5].corr()
| mean radius | mean texture | mean perimeter | mean area | mean smoothness | |
|---|---|---|---|---|---|
| mean radius | 1.000000 | 0.323782 | 0.997855 | 0.987357 | 0.170581 |
| mean texture | 0.323782 | 1.000000 | 0.329533 | 0.321086 | -0.023389 |
| mean perimeter | 0.997855 | 0.329533 | 1.000000 | 0.986507 | 0.207278 |
| mean area | 0.987357 | 0.321086 | 0.986507 | 1.000000 | 0.177028 |
| mean smoothness | 0.170581 | -0.023389 | 0.207278 | 0.177028 | 1.000000 |
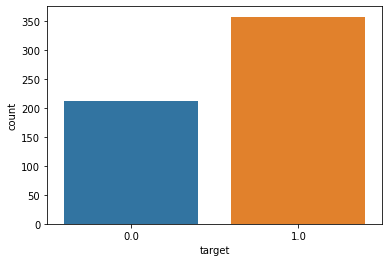
# 타겟 컬럼의 값은 각각 몇개씩인지, 차트로 나타내세요.
sb.countplot(data = df,x = df['target'])
plt.show()
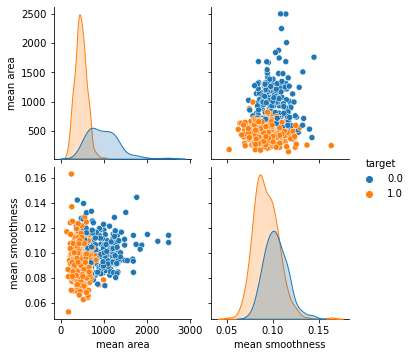
# mean area 와 mean smoothness 의 관계를 차트로 나타내세요.
# 단, target 의 데이터를 hue 에 셋팅하세요.
sb.pairplot(data = df, vars = ['mean area','mean smoothness'],hue= 'target')
plt.show()
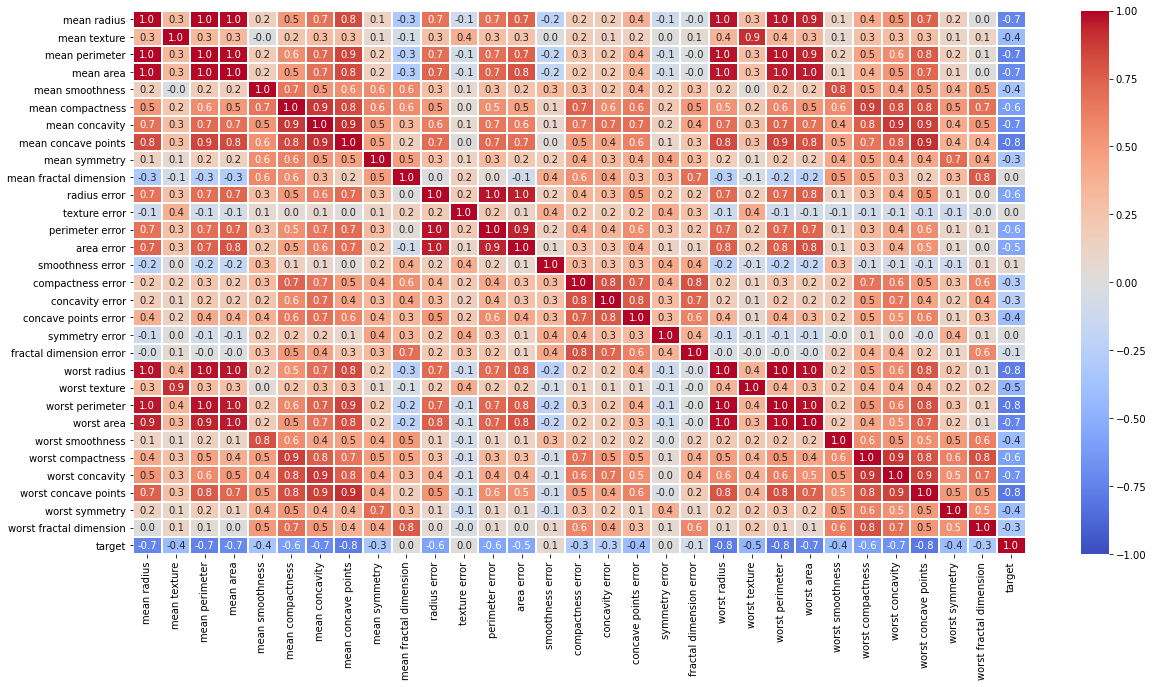
# 상관계수를 히트맵으로 보여주세요.
# 단 , cmap 은 'coolwarm'으로 세팅하세요.
df_corr = df.corr()
plt.figure(figsize=(20,10))
sb.heatmap(data=df_corr,cmap='coolwarm',annot = True,fmt='.1f',linewidths=1,vmin= -1,vmax = 1)
plt.show()
STEP #4: MODEL TRAINING (FINDING A PROBLEM SOLUTION)
X = df.iloc[:,0:-2+1]
y = df['target']
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2, random_state=5)
X.shape
(569, 30)
X_train.shape
(455, 30)
X_test.shape
(114, 30)
y_train.shape
(455,)
y_test.shape
(114,)
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix, accuracy_score, classification_report
classifier = SVC()
classifier.fit(X_train,y_train)
SVC()
STEP #5: EVALUATING THE MODEL
y_pred = classifier.predict(X_test)
confusion_matrix(y_test,y_pred)
array([[41, 7],
[ 0, 66]], dtype=int64)
accuracy_score(y_test,y_pred)
0.9385964912280702
STEP #6: IMPROVING THE MODEL
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2, random_state=5)
classifier = SVC()
classifier.fit(X_train,y_train)
SVC()
y_pred = classifier.predict(X_test)
confusion_matrix(y_test,y_pred)
array([[45, 3],
[ 1, 65]], dtype=int64)
accuracy_score(y_test,y_pred)
0.9649122807017544
print(classification_report(y_test,y_pred))
precision recall f1-score support
0.0 0.98 0.94 0.96 48
1.0 0.96 0.98 0.97 66
accuracy 0.96 114
macro avg 0.97 0.96 0.96 114
weighted avg 0.97 0.96 0.96 114
IMPROVING THE MODEL - PART 2
# grid search
para_grid = {'C':[0.1,1,10,100],'kernel':['rbf','linear'],'gamma':[1,0.1,0.01] }
from sklearn.model_selection import GridSearchCV
grid = GridSearchCV(SVC(),para_grid,refit=True,verbose=4 )
grid.fit(X_train,y_train)
Fitting 5 folds for each of 24 candidates, totalling 120 fits
[CV 1/5] END .....................C=0.1, gamma=1, kernel=rbf; total time= 0.0s
[CV 2/5] END .....................C=0.1, gamma=1, kernel=rbf; total time= 0.0s
[CV 3/5] END .....................C=0.1, gamma=1, kernel=rbf; total time= 0.0s
[CV 4/5] END .....................C=0.1, gamma=1, kernel=rbf; total time= 0.0s
[CV 5/5] END .....................C=0.1, gamma=1, kernel=rbf; total time= 0.0s
[CV 1/5] END ..................C=0.1, gamma=1, kernel=linear; total time= 0.0s
[CV 2/5] END ..................C=0.1, gamma=1, kernel=linear; total time= 0.0s
[CV 3/5] END ..................C=0.1, gamma=1, kernel=linear; total time= 0.0s
[CV 4/5] END ..................C=0.1, gamma=1, kernel=linear; total time= 0.0s
[CV 5/5] END ..................C=0.1, gamma=1, kernel=linear; total time= 0.0s
[CV 1/5] END ...................C=0.1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 2/5] END ...................C=0.1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 3/5] END ...................C=0.1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 4/5] END ...................C=0.1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 5/5] END ...................C=0.1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 1/5] END ................C=0.1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 2/5] END ................C=0.1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 3/5] END ................C=0.1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 4/5] END ................C=0.1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 5/5] END ................C=0.1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 1/5] END ..................C=0.1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 2/5] END ..................C=0.1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 3/5] END ..................C=0.1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 4/5] END ..................C=0.1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 5/5] END ..................C=0.1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 1/5] END ...............C=0.1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 2/5] END ...............C=0.1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 3/5] END ...............C=0.1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 4/5] END ...............C=0.1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 5/5] END ...............C=0.1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 1/5] END .......................C=1, gamma=1, kernel=rbf; total time= 0.0s
[CV 2/5] END .......................C=1, gamma=1, kernel=rbf; total time= 0.0s
[CV 3/5] END .......................C=1, gamma=1, kernel=rbf; total time= 0.0s
[CV 4/5] END .......................C=1, gamma=1, kernel=rbf; total time= 0.0s
[CV 5/5] END .......................C=1, gamma=1, kernel=rbf; total time= 0.0s
[CV 1/5] END ....................C=1, gamma=1, kernel=linear; total time= 0.0s
[CV 2/5] END ....................C=1, gamma=1, kernel=linear; total time= 0.0s
[CV 3/5] END ....................C=1, gamma=1, kernel=linear; total time= 0.0s
[CV 4/5] END ....................C=1, gamma=1, kernel=linear; total time= 0.0s
[CV 5/5] END ....................C=1, gamma=1, kernel=linear; total time= 0.0s
[CV 1/5] END .....................C=1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 2/5] END .....................C=1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 3/5] END .....................C=1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 4/5] END .....................C=1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 5/5] END .....................C=1, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 1/5] END ..................C=1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 2/5] END ..................C=1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 3/5] END ..................C=1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 4/5] END ..................C=1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 5/5] END ..................C=1, gamma=0.1, kernel=linear; total time= 0.0s
[CV 1/5] END ....................C=1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 2/5] END ....................C=1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 3/5] END ....................C=1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 4/5] END ....................C=1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 5/5] END ....................C=1, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 1/5] END .................C=1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 2/5] END .................C=1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 3/5] END .................C=1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 4/5] END .................C=1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 5/5] END .................C=1, gamma=0.01, kernel=linear; total time= 0.0s
[CV 1/5] END ......................C=10, gamma=1, kernel=rbf; total time= 0.0s
[CV 2/5] END ......................C=10, gamma=1, kernel=rbf; total time= 0.0s
[CV 3/5] END ......................C=10, gamma=1, kernel=rbf; total time= 0.0s
[CV 4/5] END ......................C=10, gamma=1, kernel=rbf; total time= 0.0s
[CV 5/5] END ......................C=10, gamma=1, kernel=rbf; total time= 0.0s
[CV 1/5] END ...................C=10, gamma=1, kernel=linear; total time= 0.0s
[CV 2/5] END ...................C=10, gamma=1, kernel=linear; total time= 0.0s
[CV 3/5] END ...................C=10, gamma=1, kernel=linear; total time= 0.0s
[CV 4/5] END ...................C=10, gamma=1, kernel=linear; total time= 0.0s
[CV 5/5] END ...................C=10, gamma=1, kernel=linear; total time= 0.0s
[CV 1/5] END ....................C=10, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 2/5] END ....................C=10, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 3/5] END ....................C=10, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 4/5] END ....................C=10, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 5/5] END ....................C=10, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 1/5] END .................C=10, gamma=0.1, kernel=linear; total time= 0.0s
[CV 2/5] END .................C=10, gamma=0.1, kernel=linear; total time= 0.0s
[CV 3/5] END .................C=10, gamma=0.1, kernel=linear; total time= 0.0s
[CV 4/5] END .................C=10, gamma=0.1, kernel=linear; total time= 0.0s
[CV 5/5] END .................C=10, gamma=0.1, kernel=linear; total time= 0.0s
[CV 1/5] END ...................C=10, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 2/5] END ...................C=10, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 3/5] END ...................C=10, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 4/5] END ...................C=10, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 5/5] END ...................C=10, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 1/5] END ................C=10, gamma=0.01, kernel=linear; total time= 0.0s
[CV 2/5] END ................C=10, gamma=0.01, kernel=linear; total time= 0.0s
[CV 3/5] END ................C=10, gamma=0.01, kernel=linear; total time= 0.0s
[CV 4/5] END ................C=10, gamma=0.01, kernel=linear; total time= 0.0s
[CV 5/5] END ................C=10, gamma=0.01, kernel=linear; total time= 0.0s
[CV 1/5] END .....................C=100, gamma=1, kernel=rbf; total time= 0.0s
[CV 2/5] END .....................C=100, gamma=1, kernel=rbf; total time= 0.0s
[CV 3/5] END .....................C=100, gamma=1, kernel=rbf; total time= 0.0s
[CV 4/5] END .....................C=100, gamma=1, kernel=rbf; total time= 0.0s
[CV 5/5] END .....................C=100, gamma=1, kernel=rbf; total time= 0.0s
[CV 1/5] END ..................C=100, gamma=1, kernel=linear; total time= 0.0s
[CV 2/5] END ..................C=100, gamma=1, kernel=linear; total time= 0.0s
[CV 3/5] END ..................C=100, gamma=1, kernel=linear; total time= 0.0s
[CV 4/5] END ..................C=100, gamma=1, kernel=linear; total time= 0.0s
[CV 5/5] END ..................C=100, gamma=1, kernel=linear; total time= 0.0s
[CV 1/5] END ...................C=100, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 2/5] END ...................C=100, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 3/5] END ...................C=100, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 4/5] END ...................C=100, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 5/5] END ...................C=100, gamma=0.1, kernel=rbf; total time= 0.0s
[CV 1/5] END ................C=100, gamma=0.1, kernel=linear; total time= 0.0s
[CV 2/5] END ................C=100, gamma=0.1, kernel=linear; total time= 0.0s
[CV 3/5] END ................C=100, gamma=0.1, kernel=linear; total time= 0.0s
[CV 4/5] END ................C=100, gamma=0.1, kernel=linear; total time= 0.0s
[CV 5/5] END ................C=100, gamma=0.1, kernel=linear; total time= 0.0s
[CV 1/5] END ..................C=100, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 2/5] END ..................C=100, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 3/5] END ..................C=100, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 4/5] END ..................C=100, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 5/5] END ..................C=100, gamma=0.01, kernel=rbf; total time= 0.0s
[CV 1/5] END ...............C=100, gamma=0.01, kernel=linear; total time= 0.0s
[CV 2/5] END ...............C=100, gamma=0.01, kernel=linear; total time= 0.0s
[CV 3/5] END ...............C=100, gamma=0.01, kernel=linear; total time= 0.0s
[CV 4/5] END ...............C=100, gamma=0.01, kernel=linear; total time= 0.0s
[CV 5/5] END ...............C=100, gamma=0.01, kernel=linear; total time= 0.0s
GridSearchCV(estimator=SVC(),
param_grid={'C': [0.1, 1, 10, 100], 'gamma': [1, 0.1, 0.01],
'kernel': ['rbf', 'linear']},
verbose=4)
best_classifier = grid.best_estimator_
# 가장 좋은 정확도 : 학습 데이터의 정확도, 테스트용 데이터로 측정한 정확도는 아니다.
grid.best_score_
0.9802197802197803
y_pred = best_classifier.predict(X_test)
confusion_matrix(y_test,y_pred)
array([[45, 3],
[ 1, 65]], dtype=int64)
# 정확도, 재현율, 정밀도, f1 스코어 확인
print(classification_report(y_test,y_pred))
precision recall f1-score support
0.0 0.98 0.94 0.96 48
1.0 0.96 0.98 0.97 66
accuracy 0.96 114
macro avg 0.97 0.96 0.96 114
weighted avg 0.97 0.96 0.96 114
댓글남기기